Zunächst wird zu dem nichtdeterministischen endlichen Automaten, der durch einen regulären Typ gegeben ist, ein deterministischer endlicher Automat konstruiert, indem Mengen von Zuständen anstelle der einzelnen Zustände betrachtet werden.
Die Definitionen von ![]() und
und
![]() werden
dann auf Zustandsmengen erweitert:
werden
dann auf Zustandsmengen erweitert:
Der folgende Algorithmus überprüft, ob ![]() gilt
gilt
1. falls nicht, dann FAIL
2. addto
3. falls möglich, einmit
in
auswählen,
sonst SUCCEED
4. einaus
auswählen
undin
durch
ersetzen
5.und
mit
und
berechnen
6. fallsmit
beliebig bereits in
, dann goto 3
7. falls nicht, dann FAIL
8. falls nicht
:
, dann FAIL
9. addto
10. goto 3Die Arbeitsweise dieses Algorithmus soll beispielhaft für die regulären Typen
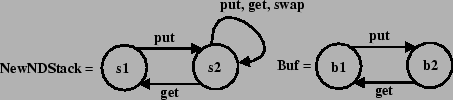
Wir beginnen mit ![]() und
und ![]() , und erhalten die folgende
Liste
, und erhalten die folgende
Liste
![]()
![]()

![]()
![]()
![]()
![]()
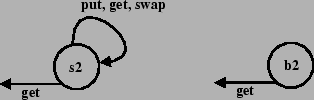
![]()
![]()
![]()
![]()
![]()
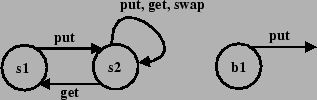
![]()
![]()
![]()
![]()
![]()
![]() ist unter 6. bereits in
ist unter 6. bereits in ![]() und unter 3. gibt es kein
und unter 3. gibt es kein ![]() mit
mit
![]() in
in ![]() mehr. Also gilt die Beziehung
mehr. Also gilt die Beziehung
![]() .
.