 |
 |
 |
Ein 2D-FFT Algorithmus läßt sich gemäß der Gleichung
 |
(16) |
unter Verwendung des 1D-FFT Algorithmus konstruieren.
Zunächst werden die Spalten der Eingabematrix durch die 1D-FFT
transformiert. Anschließend werden dann auf gleiche Weise
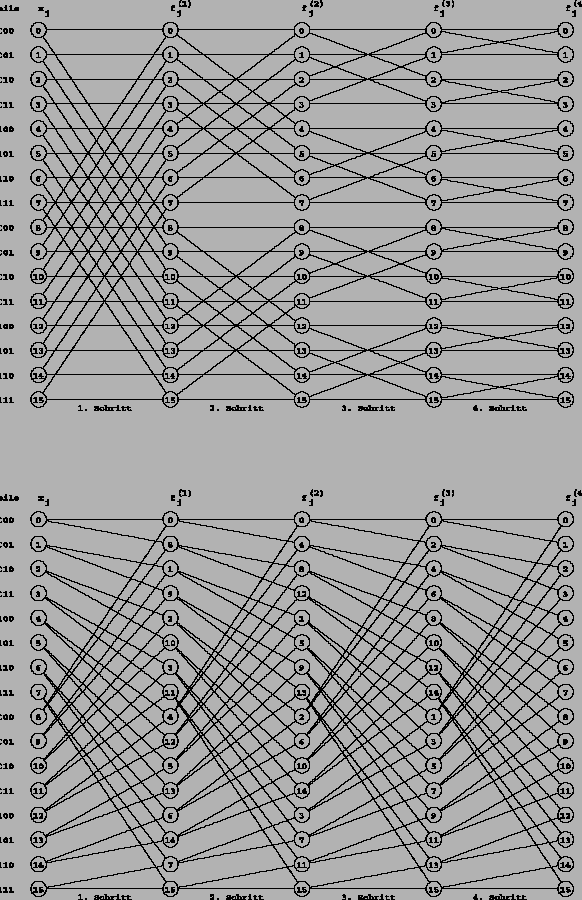
die Zeilen transformiert. Die Datenflußstruktur läßt sich wie
bei der 1D-FFT durch einen Butterfly-Graph beschreiben, in dem
jedoch jetzt in der ersten Hälfte die Spalten-
und in der zweiten die Zeilentransformationen stattfinden.
Hieraus ergeben sich andere Gewichte der Knotenfunktionen.
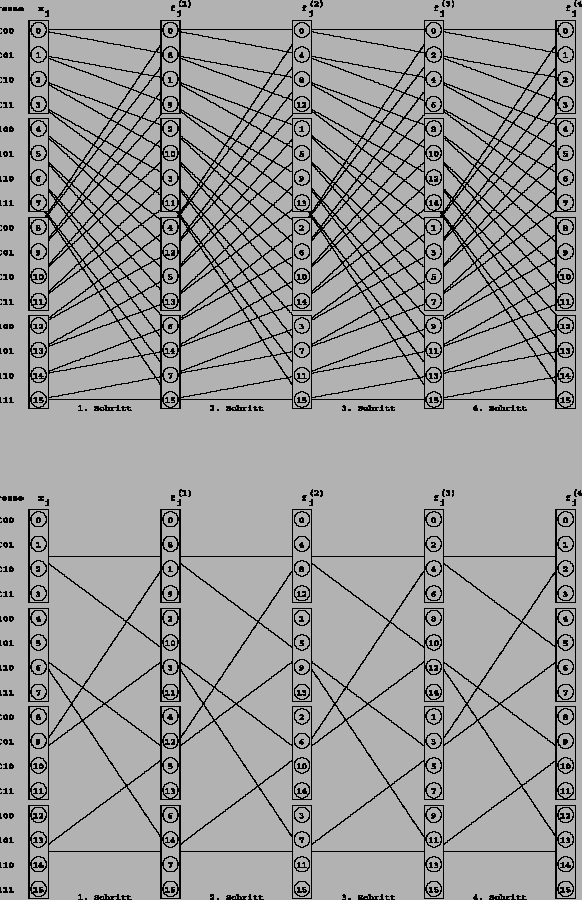
Aus der Reihenfolge der Transformationen ergibt folgende Datenverteilung
auf die Knoten des Butterfly-Graphen (Abbildung ![]() )
)
| 0 | 1 | 2 | 3 |
| 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 |
Ein paralleler 2D-FFT Algorithmus für ![]() Prozessoren auf Basis
dieses Butterfly-Graphen läßt sich wie folgt konstruieren
Prozessoren auf Basis
dieses Butterfly-Graphen läßt sich wie folgt konstruieren